week 12:

Genetic Switches

Preliminars

Present all your reasoning, derivations, plots and code as part of the homework. Imagine that you are writing a short paper that anyone in class should to be able to understand. If you are stuck in some point, please describe the issue and how far you got. A jupyter notebook if you are working in Python is not required, but recommended.

A fast and robust oscillator

In class, we discussed the repressilator by Elowitz & Leibler, a synthetic network implemented in E. coli that produces oscillations. The repressilator turned out to be not very robust, as only 40% of the cells presented oscillations. In this homework, we are going to implement a different oscillator that depends on two genes with both negative and positive feedback loops: “A fast, robust and tunable synthetic gene oscillator” by J. Stricker et al.

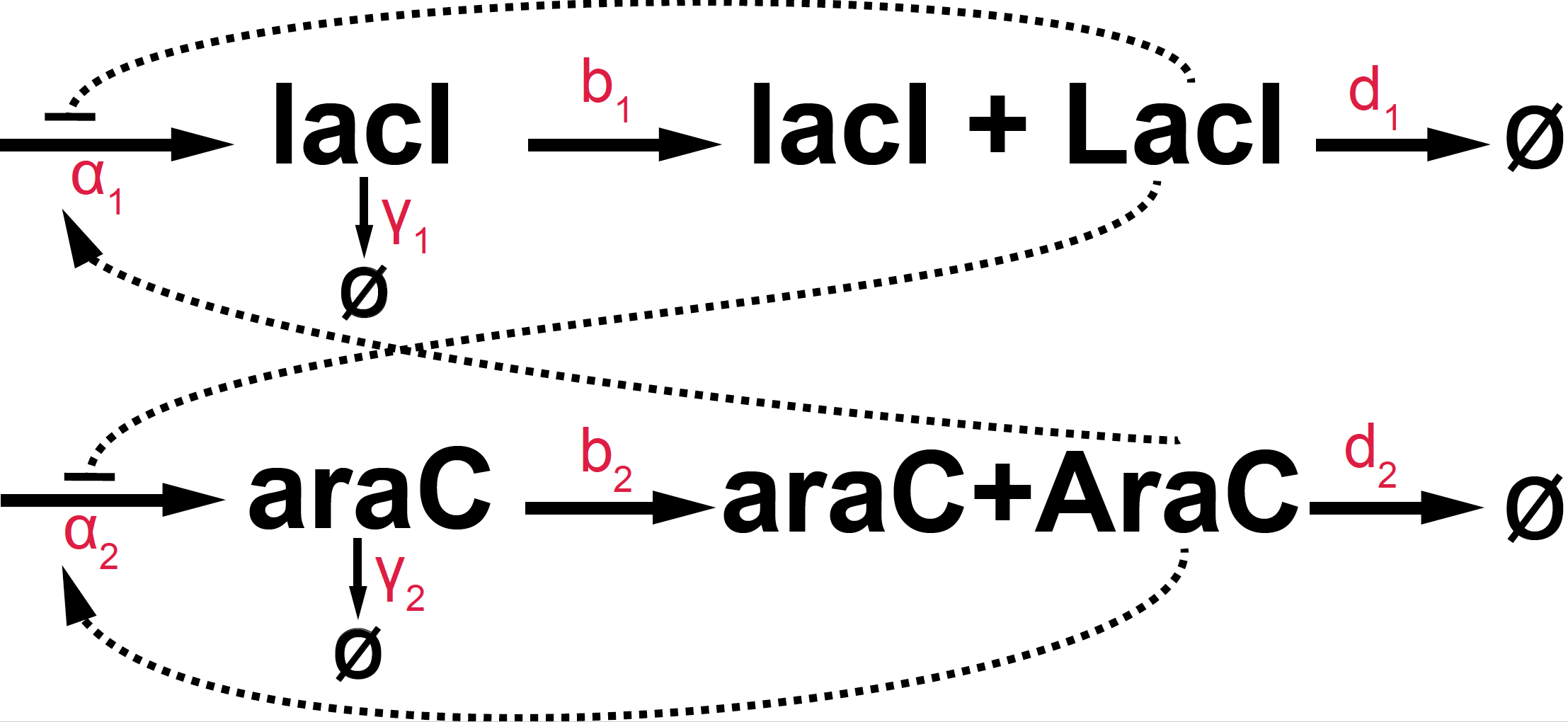
Figure 1. Basic diagram of the Stricker oscillator.

A diagramtic representation of this oscillator is given in Figure 1. In terms of the actual parameters:

We know that the LacI protein acts as a dimer, and the AraC protein acts as a tetrad, which determines the Hill coefficients for the feedback loops.
We assume enzymatic decay for all RNA and protein species with Michaelis-Menten coefficients provided bellow.

parameter	Description	value
\(\alpha_1\)	lacI RNA production	2.5
\(\alpha_2\)	araC RNA production	2.5
\(\gamma_1\)	lacI RNA degradation	0.6
\(\gamma_2\)	araC RNA degradation	0.8
\(n1\)	cooperativity coefficient of LacI binding	2
\(n2\)	cooperativity coefficient of AraC binding	4
\(K^+\)	Hill constant for LacI (-) feedback loop	2
\(K^-\)	Hill constant for AraC (+) feedback loop	0.003
\(b_1\)	lacI translation rate	0.4
\(b_2\)	araC translation rate	0.1
\(d_1\)	LacI degradation rate	0.8
\(d_2\)	AraC degradation rate	0.2
\(K\gamma 1\)	Michaelis constant for lacI RNA degradation	0.01
\(K\gamma 2\)	Michaelis constant for araC RNA degradation	0.1
\(Kd1\)	Michaelis constant for LacI degradation	0.01
\(Kd2\)	Michaelis constant for AraC degradation	0.1

Propose the kinetic equations of the system.
Solve numerically the differential equations, and plot the concentrations of the four species as a function of time, for the particular values provided in the table above.
In your hands, is this oscillator more robust (theoretically) than the repressilator?
Do you need the Michaelis-Menten enzymatic degradation for the system to oscillate?
Can you identify one parameter important to maintain the oscillatory behavior? What is the range of parameters for which there are oscillations.
Which parameter would you use to control the period of the oscillations?
If you remove the araC gene, does the lacI system with just one negative feedback loop oscillate? How that is compare to the two-gene system of Stricker?
The Stricker et al. implementation is slightly different from this one. You can see the details in their supplemental materials. How does your implementation compare to Stricker’s?