MCB111: Mathematics in Biology (Fall 2024)
week 01:
The length of a unique sequence in a genome
In a genome of length \(L\), what is the shortest sequence (motif) that we expect to appear only once?
An alternative way of asking the same question: how long has to be a motif for it to match only one location in the genome?
Eukaryotic genomes have on the order of \(L=10^{6}-10^{10}\) nucleotides. We assume that the length of the motif is \(l\). Let’s also assume a that the base composition of the genome is such that all four bases (A, C, G, T) are equally likely. Then, a motif of length \(l=1\) (for instance “A”), will match \(1/4\) of the positions in the genome. If we take a motif of length \(l=2\), for instance “AA” it will match fewer than \(1/4\), but not much better.
How do we address this question?
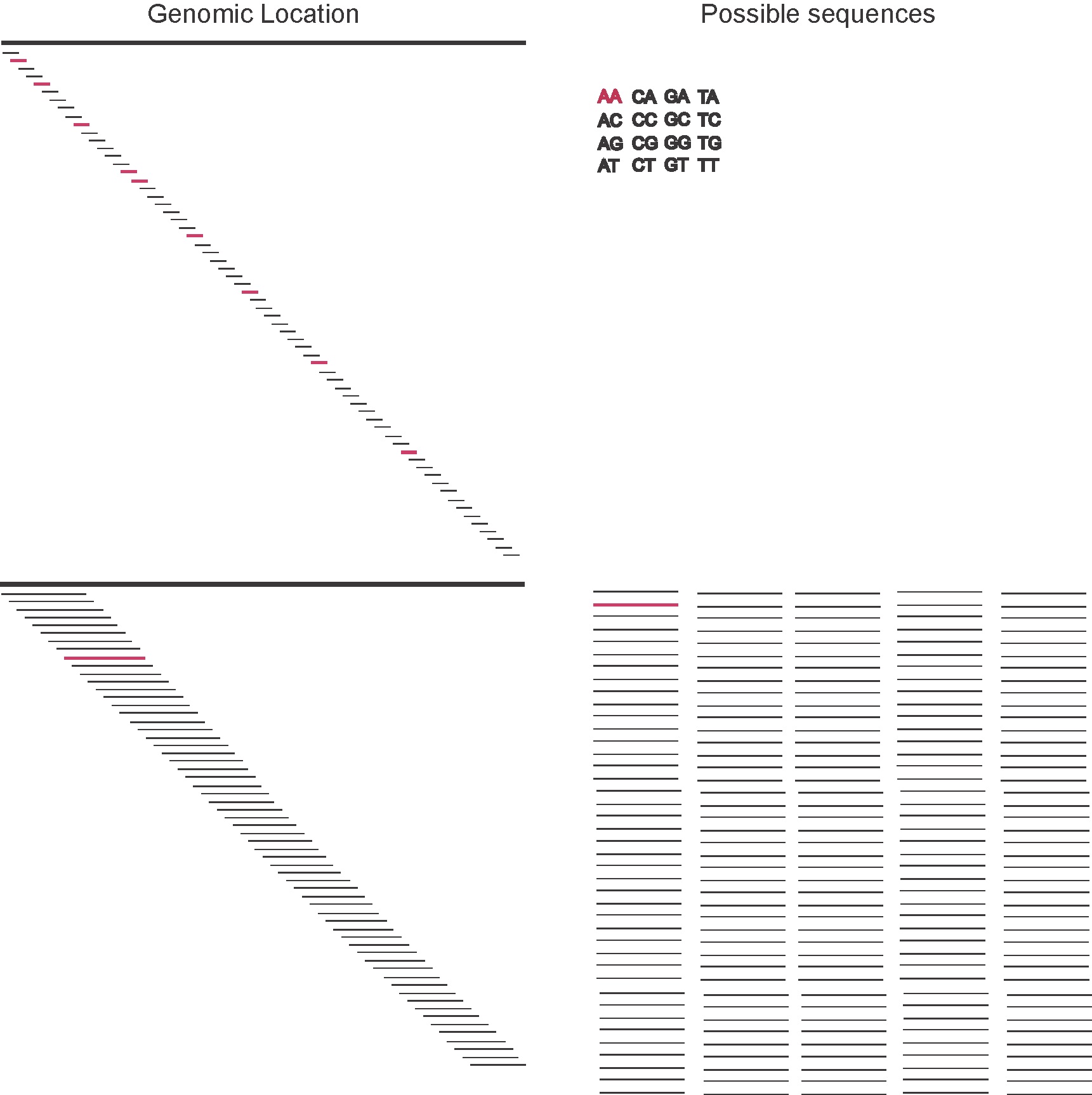
Figure 2. The ignorance about the location in the genome is determined by the length of the genome L as log_2(L), and it doesn't depend on the length of the motif l (as long as l<<L and we can ignore edges). The total number of possible motifs is 4^l, and the information content of each one of them is log_2(4^l)= 2l (assuming all residues are equally likely). In a situation where the segment size is small, the total number of possible segments is small (for instance, for l=2 there are 16 possible segments), thus we expect that none of the segments is going to be unique in the genome. As the segment size increases, the number of possible segments does too, so does the information content of each one of them (for instance, for l=16 there are over 4 billion possible segments) then it becomes more likely that a given segment is unique in the genome.
-
On the one hand, we have the information of where the sequence is going to land in the genome (the genomic position), if we assume all \(L\) positions are equally likely we have, then a given motif can fall starting at any of the \(L\) positions in the genome. (The exact nubmer of starting positions for a motif of length \(l\) is \(L-l\), but it we assume \(l<< L\) then \(L-l\approx L\).)
Then, the information in the genome position of the motif is
\[\log_2 L\] -
On the other hand, we have the information in the motif. That is, using a combination of A, C, G, T’s how many different motifs can we make that have length \(l\)
If we assume that each position is independent from each other, so their entropies add up, and each position can be one of the four residues, so the number of possibilities for one position is 4, and
Information content on a motif with l positions is
\[I(l) = l\ \log_2(4) = 2\ l\]Since the probability of each nucleic acid is
\[p_A = p_C = p_G = p_T = \frac{1}{4}\]we can re-written the information of the motif as
\[I(l) = 2\ l = l\ \log_2(4) = l\ \log_2\frac{1}{1/4},\]that is, the sum of the information content of \(l\) sites each with probability \(\frac{1}{4}\).
For the motif to be unique, we want the information on the motif composition to be at least as large as that of the possible location of the motif, that is We want to have the condition (see Figure 2)
\[\mbox{Information( motif)}\quad >=\quad \mbox{Information(genome position)}\]or
\[H(l) >= \log_2(L)\]that we require that the length of the motif \(l\) is at least
\[l = \frac{1}{2}\ log_2(L)\]Let’s check the result by simulation
Let’s look at some examples. Assume a genome of length \(L = 10^6\).
-
The theoretical results
The ``location information’’ is \(\log_2{10^6}=19.93\, \mbox{bits},\)
and the entropy for different motifs of different lengths are
| length | l=4 | l=4 | l=6 | l=6 | l = 10 | l= 10 |
|---|---|---|---|---|---|---|
| motif | AAAA | CCCC | AAAAAA | CCCCCC | AAAAAAAAAA | CCCCCCCCCC |
| I(motif) | 8.0 | 8.0 | 12.0 | 12.0 | 20.0 | 20.0 |
In bold, situations in which the motif’s information is larger than the genome position information, and we should expect the motif to be unique in the genome.
For a genome where all nucleotides are distributed equally and for a genome of length \(10^6\), sequences of length \(10\) or larger will already be unique.
- A simulation
Here, I simulate random genomes of length \(10^6\), and we calculate how many times the different motifs were found. By generating several different genomes, we can also estimate the mean and variance.
Here are actual results using 20 random genomes, and assuming that all nucleotides have the same probability \(1/4\),
| lenght | l=4 | l=4 | l=6 | l=6 | l = 10 | l= 10 |
|---|---|---|---|---|---|---|
| motif | AAAA | CCCC | AAAAAA | CCCCCC | AAAAAAAAAA | CCCCCCCCCC |
| occurence | 3,894\(\pm\)88 | 3,904\(\pm\)93 | 240\(\pm\)13 | 247\(\pm\)25 | 1.2\(\pm\)1.2 | 0.9\(\pm\)1.2 |
As a rule of thumb, for a genome with residues uniformly distributed (\(p_A=p_C=p_G=p_T=0.25\)), then the information content of a nucleotide is 2 bits (\(\log_2\frac{1}{0.25}\)) and the length of a unique motif is \begin{equation} l \geq \frac{\log_2(L)}{2}. \end{equation}
Some examples,
| genome | length \(L\) | genome inf content | unique motif length \(l\) |
|---|---|---|---|
| human | \(4\times 10^9\) | 32 bits | 16 |
| worm | \(100\times 10^6\) | 27 bits | 13 |
| E.coli | \(6\times 10^6\) | 22 bits | 11 |